Here I will be developing a model for prediction of handwritten digits using famous MNIST dataset. I will build first model using Support Vector Machine(SVM) followed by an improved approach using Principal Component Analysis(PCA).
Fetching Data
#Loading train & test data, the datasets were obtained from kaggle: https://www.kaggle.com/c/digit-recognizer/data
mnist <- read.csv("train.csv")
mnist_test <- read.csv("test.csv")
Checking dataset dimensions
dim(mnist)
## [1] 42000 785
#train dataset have 42000 images & 785 columns(784 representing 28x28 pixels image, 1 representing image class)
dim(mnist_test)
## [1] 28000 784
#train dataset have 28000 images & 784 columns(784 representing 28x28 pixels image)
Lets check distribution percentage of each digit in train dataset
table(mnist$label)/nrow(mnist) *100
##
## 0 1 2 3 4 5 6
## 9.838095 11.152381 9.945238 10.359524 9.695238 9.035714 9.850000
## 7 8 9
## 10.478571 9.673810 9.971429
#Have uniform distribution of each digit
Visualizing a digit in data
digit <- matrix(as.numeric(mnist[4,-1]), nrow = 28)
image(digit, col = grey.colors(255))
#This is how a typical digit looks in our dataset, image is flipped
Some more images of same digit to show the variations in handwriting
mnist_copy<-mnist
mnist_copy_7 <- mnist_copy[mnist_copy$label == 7, ]
flip <- function(matrix){
apply(matrix, 2, rev)
}
#Shows 9 diffrent ways people write digit 7
par(mfrow=c(3,3))
for (i in 10:18){
digit <- flip(matrix(rev(as.numeric(mnist_copy_7[i,-c(1, 786)])), nrow = 28)) #shows different styles of digit
image(digit, col = grey.colors(255))
}
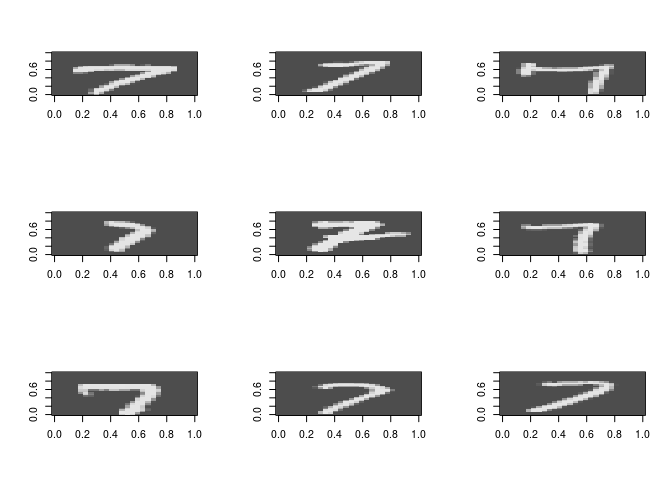
Preparing to build the model
#Lets first convert our class label to factor or categorical type
mnist$label <-factor(mnist$label)
#Dividing data into training & validation sets
set.seed(100)
indices = sample.split(mnist$label, SplitRatio = 0.2)
train = mnist[indices,]
test = mnist[-indices,]
Building a model for predicting handwritten image using SVM
#I have skipped hyper-parameter tunning here as its compute intensive
Model_RBF <- ksvm(label~., data = train, scale = FALSE, kernel = "rbfdot")
## Warning in .local(x, ...): Variable(s) `' constant. Cannot scale data.
Eval_RBF<- predict(Model_RBF, test)
#confusion matrix - RBF Kernel
confusionMatrix(Eval_RBF,test$label)
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1 2 3 4 5 6 7 8 9
## 0 4081 0 17 6 5 19 28 6 7 18
## 1 0 4612 14 15 9 7 1 34 44 11
## 2 8 23 4023 69 20 18 4 36 18 11
## 3 2 14 15 4079 0 59 0 2 41 58
## 4 6 7 27 2 3925 8 11 25 25 66
## 5 10 6 7 79 3 3631 24 4 45 15
## 6 13 1 10 8 13 31 4063 0 12 1
## 7 1 5 31 23 5 4 0 4208 19 59
## 8 10 11 28 47 1 9 6 4 3825 30
## 9 1 4 5 23 91 9 0 82 27 3919
##
## Overall Statistics
##
## Accuracy : 0.9611
## 95% CI : (0.9592, 0.9629)
## No Information Rate : 0.1115
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.9568
## Mcnemar's Test P-Value : NA
##
## Statistics by Class:
##
## Class: 0 Class: 1 Class: 2 Class: 3 Class: 4 Class: 5
## Sensitivity 0.98766 0.9848 0.96313 0.93749 0.96390 0.95679
## Specificity 0.99720 0.9964 0.99453 0.99493 0.99533 0.99495
## Pos Pred Value 0.97468 0.9716 0.95106 0.95527 0.95685 0.94953
## Neg Pred Value 0.99865 0.9981 0.99592 0.99279 0.99612 0.99570
## Prevalence 0.09838 0.1115 0.09945 0.10360 0.09695 0.09036
## Detection Rate 0.09717 0.1098 0.09579 0.09712 0.09345 0.08645
## Detection Prevalence 0.09969 0.1130 0.10072 0.10167 0.09767 0.09105
## Balanced Accuracy 0.99243 0.9906 0.97883 0.96621 0.97962 0.97587
## Class: 6 Class: 7 Class: 8 Class: 9
## Sensitivity 0.98211 0.9561 0.94142 0.93577
## Specificity 0.99765 0.9961 0.99615 0.99360
## Pos Pred Value 0.97856 0.9662 0.96323 0.94184
## Neg Pred Value 0.99804 0.9949 0.99374 0.99289
## Prevalence 0.09850 0.1048 0.09674 0.09972
## Detection Rate 0.09674 0.1002 0.09107 0.09331
## Detection Prevalence 0.09886 0.1037 0.09455 0.09907
## Balanced Accuracy 0.98988 0.9761 0.96879 0.96468
Lets try PCA now
#Reducing features using PCA
mnist_norm<-as.matrix(mnist[,-1])/255
mnist_norm_cov <- cov(mnist_norm)
pca <- prcomp(mnist_norm_cov)
trainlabel <- mnist[,1]
#Checking relationship between number of Pricipal Components & Variance
vexplained <- as.data.frame(pca$sdev^2/sum(pca$sdev^2))
vexplained <- cbind(c(1:784),vexplained,cumsum(vexplained[,1]))
colnames(vexplained) <- c("No_of_Principal_Components","Individual_Variance_Explained","Cumulative_Variance_Explained")
#Plot between Cumulative Variance & Principal Components
plot(vexplained$No_of_Principal_Components,vexplained$Cumulative_Variance_Explained, xlim = c(0,150),type='b',pch=16,xlab = "Principal Componets",ylab = "Cumulative Variance Explained",main = 'Principal Components vs Cumulative Variance Explained')
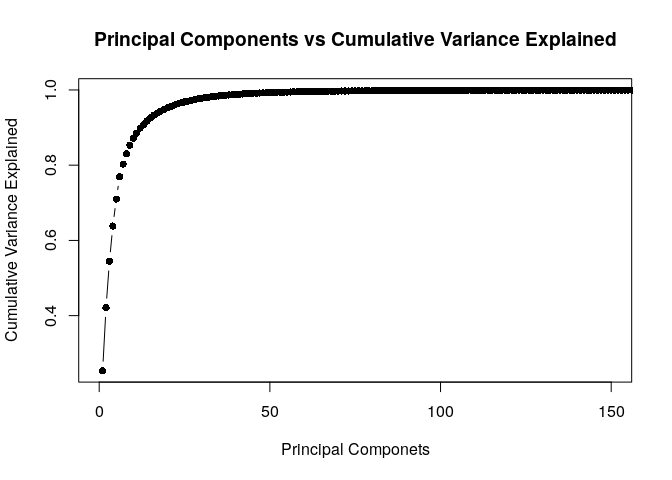
Table showing Cumulative Variance & Principal Components
vexplainedsummary <- vexplained[seq(0,150,5),]
kable(vexplainedsummary)
| No_of_Principal_Components | Individual_Variance_Explained | Cumulative_Variance_Explained | |
|---|---|---|---|
| 5 | 5 | 0.0716813 | 0.7099512 |
| 10 | 10 | 0.0180431 | 0.8711603 |
| 15 | 15 | 0.0081399 | 0.9256031 |
| 20 | 20 | 0.0043323 | 0.9527282 |
| 25 | 25 | 0.0025642 | 0.9682100 |
| 30 | 30 | 0.0015399 | 0.9779664 |
| 35 | 35 | 0.0010429 | 0.9840624 |
| 40 | 40 | 0.0007112 | 0.9880982 |
| 45 | 45 | 0.0004829 | 0.9909898 |
| 50 | 50 | 0.0003355 | 0.9929776 |
| 55 | 55 | 0.0002571 | 0.9944191 |
| 60 | 60 | 0.0001985 | 0.9955116 |
| 65 | 65 | 0.0001498 | 0.9963654 |
| 70 | 70 | 0.0001163 | 0.9970027 |
| 75 | 75 | 0.0000902 | 0.9975132 |
| 80 | 80 | 0.0000663 | 0.9978984 |
| 85 | 85 | 0.0000573 | 0.9982081 |
| 90 | 90 | 0.0000468 | 0.9984654 |
| 95 | 95 | 0.0000382 | 0.9986709 |
| 100 | 100 | 0.0000327 | 0.9988451 |
| 105 | 105 | 0.0000269 | 0.9989884 |
| 110 | 110 | 0.0000218 | 0.9991066 |
| 115 | 115 | 0.0000188 | 0.9992046 |
| 120 | 120 | 0.0000161 | 0.9992906 |
| 125 | 125 | 0.0000141 | 0.9993654 |
| 130 | 130 | 0.0000120 | 0.9994293 |
| 135 | 135 | 0.0000108 | 0.9994860 |
| 140 | 140 | 0.0000090 | 0.9995354 |
| 145 | 145 | 0.0000080 | 0.9995773 |
| 150 | 150 | 0.0000071 | 0.9996148 |
#Note: Variance till Number of Principal Components 45 is 0.9909898
Applying SVM on training set and calculating accuracy using top 45 principal components
mnist_final <- as.matrix(mnist[,-1]) %*% pca$x[,1:45]
trainlabel <- as.factor(trainlabel)
svm.model.final <- svm(mnist_final,trainlabel,cost = 2)
predictionfinaltrain <- predict(svm.model.final,mnist_final)
correcttrainfinal <- predictionfinaltrain==trainlabel
Accuracytrainfinal <- (sum(correcttrainfinal)/nrow(mnist_final))*100
Accuracytrainfinal #99.70 %
## [1] 99.70238
Predicting mnist test data labels using above model
mnist_test_pca<-as.matrix(mnist_test) %*% pca$x[,1:45]
mnist_predictions<-predict(svm.model.final,mnist_test_pca)
mnist_test$predicted_labels<-mnist_predictions
mnist_test$predicted_labels[1:10]
## [1] 2 0 9 9 3 7 0 3 0 3
## Levels: 0 1 2 3 4 5 6 7 8 9
#Testing a predicted label manually, Digit 3 on 8th record is correctly predicted.
digit <- matrix(as.numeric(mnist_test[8,-785]), nrow = 28)
image(digit, col = grey.colors(255))
#I get a decent accuracy of 98.4% using this model on kaggle, but can we do better?