
Image Source
About dataset:
I took this dataset from kaggle(https://www.kaggle.com/mig555/mushroom-classification/data) though it was originally contributed to the UCI Machine Learning repository nearly 30 years ago.
This dataset includes descriptions of hypothetical samples corresponding to 23 species of gilled mushrooms in the Agaricus and Lepiota Family Mushroom drawn from The Audubon Society Field Guide to North American Mushrooms (1981). Each species is identified as definitely edible, definitely poisonous, or of unknown edibility and not recommended. This latter class was combined with the poisonous one. The Guide clearly states that there is no simple rule for determining the edibility of a mushroom; no rule like “leaflets three, let it be’’ for Poisonous Oak and Ivy.
Problem & Approach:
To develop a binary classifier to predict which mushroom is poisonous & which is edible. I will build a Naive Bayes classifier for prediction after basic EDA of data. Later I will also test Decision Tree & Random Forest models on this dataset.
Lets check data structure
str(mushroom)
## 'data.frame': 8124 obs. of 23 variables:
## $ class : Factor w/ 2 levels "e","p": 2 1 1 2 1 1 1 1 2 1 ...
## $ cap.shape : Factor w/ 6 levels "b","c","f","k",..: 6 6 1 6 6 6 1 1 6 1 ...
## $ cap.surface : Factor w/ 4 levels "f","g","s","y": 3 3 3 4 3 4 3 4 4 3 ...
## $ cap.color : Factor w/ 10 levels "b","c","e","g",..: 5 10 9 9 4 10 9 9 9 10 ...
## $ bruises : Factor w/ 2 levels "f","t": 2 2 2 2 1 2 2 2 2 2 ...
## $ odor : Factor w/ 9 levels "a","c","f","l",..: 7 1 4 7 6 1 1 4 7 1 ...
## $ gill.attachment : Factor w/ 2 levels "a","f": 2 2 2 2 2 2 2 2 2 2 ...
## $ gill.spacing : Factor w/ 2 levels "c","w": 1 1 1 1 2 1 1 1 1 1 ...
## $ gill.size : Factor w/ 2 levels "b","n": 2 1 1 2 1 1 1 1 2 1 ...
## $ gill.color : Factor w/ 12 levels "b","e","g","h",..: 5 5 6 6 5 6 3 6 8 3 ...
## $ stalk.shape : Factor w/ 2 levels "e","t": 1 1 1 1 2 1 1 1 1 1 ...
## $ stalk.root : Factor w/ 5 levels "?","b","c","e",..: 4 3 3 4 4 3 3 3 4 3 ...
## $ stalk.surface.above.ring: Factor w/ 4 levels "f","k","s","y": 3 3 3 3 3 3 3 3 3 3 ...
## $ stalk.surface.below.ring: Factor w/ 4 levels "f","k","s","y": 3 3 3 3 3 3 3 3 3 3 ...
## $ stalk.color.above.ring : Factor w/ 9 levels "b","c","e","g",..: 8 8 8 8 8 8 8 8 8 8 ...
## $ stalk.color.below.ring : Factor w/ 9 levels "b","c","e","g",..: 8 8 8 8 8 8 8 8 8 8 ...
## $ veil.type : Factor w/ 1 level "p": 1 1 1 1 1 1 1 1 1 1 ...
## $ veil.color : Factor w/ 4 levels "n","o","w","y": 3 3 3 3 3 3 3 3 3 3 ...
## $ ring.number : Factor w/ 3 levels "n","o","t": 2 2 2 2 2 2 2 2 2 2 ...
## $ ring.type : Factor w/ 5 levels "e","f","l","n",..: 5 5 5 5 1 5 5 5 5 5 ...
## $ spore.print.color : Factor w/ 9 levels "b","h","k","n",..: 3 4 4 3 4 3 3 4 3 3 ...
## $ population : Factor w/ 6 levels "a","c","n","s",..: 4 3 3 4 1 3 3 4 5 4 ...
## $ habitat : Factor w/ 7 levels "d","g","l","m",..: 6 2 4 6 2 2 4 4 2 4 ...
Renaming all entities
As you might have noticed all data entities are named by initials only. Lets convert these to proper names for clarity & also convert all attributes to factors as all attributes are categorical here.
colnames(mushroom) <- c("Edibility", "CapShape", "CapSurface",
"CapColor", "Bruises", "Odor",
"GillAttachment", "GillSpacing", "GillSize",
"GillColor", "StalkShape", "StalkRoot",
"StalkSurfaceAboveRing", "StalkSurfaceBelowRing", "StalkColorAboveRing",
"StalkColorBelowRing", "VeilType", "VeilColor",
"RingNumber", "RingType", "SporePrintColor",
"Population", "Habitat")
mushroom <- mushroom %>% map_df(function(.x) as.factor(.x))
levels(mushroom$Edibility) <- c("edible", "poisonous")
levels(mushroom$CapShape) <- c("bell", "conical", "flat", "knobbed", "sunken", "convex")
levels(mushroom$CapColor) <- c("buff", "cinnamon", "red", "gray", "brown", "pink",
"green", "purple", "white", "yellow")
levels(mushroom$CapSurface) <- c("fibrous", "grooves", "scaly", "smooth")
levels(mushroom$Bruises) <- c("no", "yes")
levels(mushroom$Odor) <- c("almond", "creosote", "foul", "anise", "musty", "none", "pungent", "spicy", "fishy")
levels(mushroom$GillAttachment) <- c("attached", "free")
levels(mushroom$GillSpacing) <- c("close", "crowded")
levels(mushroom$GillSize) <- c("broad", "narrow")
levels(mushroom$GillColor) <- c("buff", "red", "gray", "chocolate", "black", "brown", "orange",
"pink", "green", "purple", "white", "yellow")
levels(mushroom$StalkShape) <- c("enlarging", "tapering")
levels(mushroom$StalkRoot) <- c("missing", "bulbous", "club", "equal", "rooted")
levels(mushroom$StalkSurfaceAboveRing) <- c("fibrous", "silky", "smooth", "scaly")
levels(mushroom$StalkSurfaceBelowRing) <- c("fibrous", "silky", "smooth", "scaly")
levels(mushroom$StalkColorAboveRing) <- c("buff", "cinnamon", "red", "gray", "brown", "pink",
"green", "purple", "white", "yellow")
levels(mushroom$StalkColorBelowRing) <- c("buff", "cinnamon", "red", "gray", "brown", "pink",
"green", "purple", "white", "yellow")
levels(mushroom$VeilType) <- "partial"
levels(mushroom$VeilColor) <- c("brown", "orange", "white", "yellow")
levels(mushroom$RingNumber) <- c("none", "one", "two")
levels(mushroom$RingType) <- c("evanescent", "flaring", "large", "none", "pendant")
levels(mushroom$SporePrintColor) <- c("buff", "chocolate", "black", "brown", "orange",
"green", "purple", "white", "yellow")
levels(mushroom$Population) <- c("abundant", "clustered", "numerous", "scattered", "several", "solitary")
levels(mushroom$Habitat) <- c("wood", "grasses", "leaves", "meadows", "paths", "urban", "waste")
Lets check few records from dataset now
head(mushroom) %>% kable("html") %>%
kable_styling()
| Edibility | CapShape | CapSurface | CapColor | Bruises | Odor | GillAttachment | GillSpacing | GillSize | GillColor | StalkShape | StalkRoot | StalkSurfaceAboveRing | StalkSurfaceBelowRing | StalkColorAboveRing | StalkColorBelowRing | VeilType | VeilColor | RingNumber | RingType | SporePrintColor | Population | Habitat |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| poisonous | convex | scaly | brown | yes | pungent | free | close | narrow | black | enlarging | equal | smooth | smooth | purple | purple | partial | white | one | pendant | black | scattered | urban |
| edible | convex | scaly | yellow | yes | almond | free | close | broad | black | enlarging | club | smooth | smooth | purple | purple | partial | white | one | pendant | brown | numerous | grasses |
| edible | bell | scaly | white | yes | anise | free | close | broad | brown | enlarging | club | smooth | smooth | purple | purple | partial | white | one | pendant | brown | numerous | meadows |
| poisonous | convex | smooth | white | yes | pungent | free | close | narrow | brown | enlarging | equal | smooth | smooth | purple | purple | partial | white | one | pendant | black | scattered | urban |
| edible | convex | scaly | gray | no | none | free | crowded | broad | black | tapering | equal | smooth | smooth | purple | purple | partial | white | one | evanescent | brown | abundant | grasses |
| edible | convex | smooth | yellow | yes | almond | free | close | broad | brown | enlarging | club | smooth | smooth | purple | purple | partial | white | one | pendant | black | numerous | grasses |
Lets check the structure of data now
str(mushroom)
## Classes 'tbl_df', 'tbl' and 'data.frame': 8124 obs. of 23 variables:
## $ Edibility : Factor w/ 2 levels "edible","poisonous": 2 1 1 2 1 1 1 1 2 1 ...
## $ CapShape : Factor w/ 6 levels "bell","conical",..: 6 6 1 6 6 6 1 1 6 1 ...
## $ CapSurface : Factor w/ 4 levels "fibrous","grooves",..: 3 3 3 4 3 4 3 4 4 3 ...
## $ CapColor : Factor w/ 10 levels "buff","cinnamon",..: 5 10 9 9 4 10 9 9 9 10 ...
## $ Bruises : Factor w/ 2 levels "no","yes": 2 2 2 2 1 2 2 2 2 2 ...
## $ Odor : Factor w/ 9 levels "almond","creosote",..: 7 1 4 7 6 1 1 4 7 1 ...
## $ GillAttachment : Factor w/ 2 levels "attached","free": 2 2 2 2 2 2 2 2 2 2 ...
## $ GillSpacing : Factor w/ 2 levels "close","crowded": 1 1 1 1 2 1 1 1 1 1 ...
## $ GillSize : Factor w/ 2 levels "broad","narrow": 2 1 1 2 1 1 1 1 2 1 ...
## $ GillColor : Factor w/ 12 levels "buff","red","gray",..: 5 5 6 6 5 6 3 6 8 3 ...
## $ StalkShape : Factor w/ 2 levels "enlarging","tapering": 1 1 1 1 2 1 1 1 1 1 ...
## $ StalkRoot : Factor w/ 5 levels "missing","bulbous",..: 4 3 3 4 4 3 3 3 4 3 ...
## $ StalkSurfaceAboveRing: Factor w/ 4 levels "fibrous","silky",..: 3 3 3 3 3 3 3 3 3 3 ...
## $ StalkSurfaceBelowRing: Factor w/ 4 levels "fibrous","silky",..: 3 3 3 3 3 3 3 3 3 3 ...
## $ StalkColorAboveRing : Factor w/ 10 levels "buff","cinnamon",..: 8 8 8 8 8 8 8 8 8 8 ...
## $ StalkColorBelowRing : Factor w/ 10 levels "buff","cinnamon",..: 8 8 8 8 8 8 8 8 8 8 ...
## $ VeilType : Factor w/ 1 level "partial": 1 1 1 1 1 1 1 1 1 1 ...
## $ VeilColor : Factor w/ 4 levels "brown","orange",..: 3 3 3 3 3 3 3 3 3 3 ...
## $ RingNumber : Factor w/ 3 levels "none","one","two": 2 2 2 2 2 2 2 2 2 2 ...
## $ RingType : Factor w/ 5 levels "evanescent","flaring",..: 5 5 5 5 1 5 5 5 5 5 ...
## $ SporePrintColor : Factor w/ 9 levels "buff","chocolate",..: 3 4 4 3 4 3 3 4 3 3 ...
## $ Population : Factor w/ 6 levels "abundant","clustered",..: 4 3 3 4 1 3 3 4 5 4 ...
## $ Habitat : Factor w/ 7 levels "wood","grasses",..: 6 2 4 6 2 2 4 4 2 4 ...
Lets find out more about each category of each attribute
summary(mushroom)
## Edibility CapShape CapSurface CapColor Bruises
## edible :4208 bell : 452 fibrous:2320 brown :2284 no :4748
## poisonous:3916 conical: 4 grooves: 4 gray :1840 yes:3376
## flat :3152 scaly :2556 red :1500
## knobbed: 828 smooth :3244 yellow :1072
## sunken : 32 white :1040
## convex :3656 buff : 168
## (Other): 220
## Odor GillAttachment GillSpacing GillSize
## none :3528 attached: 210 close :6812 broad :5612
## foul :2160 free :7914 crowded:1312 narrow:2512
## spicy : 576
## fishy : 576
## almond : 400
## anise : 400
## (Other): 484
## GillColor StalkShape StalkRoot StalkSurfaceAboveRing
## buff :1728 enlarging:3516 missing:2480 fibrous: 552
## pink :1492 tapering :4608 bulbous:3776 silky :2372
## white :1202 club : 556 smooth :5176
## brown :1048 equal :1120 scaly : 24
## gray : 752 rooted : 192
## chocolate: 732
## (Other) :1170
## StalkSurfaceBelowRing StalkColorAboveRing StalkColorBelowRing
## fibrous: 600 purple :4464 purple :4384
## silky :2304 green :1872 green :1872
## smooth :4936 gray : 576 gray : 576
## scaly : 284 brown : 448 brown : 512
## buff : 432 buff : 432
## pink : 192 pink : 192
## (Other): 140 (Other): 156
## VeilType VeilColor RingNumber RingType
## partial:8124 brown : 96 none: 36 evanescent:2776
## orange: 96 one :7488 flaring : 48
## white :7924 two : 600 large :1296
## yellow: 8 none : 36
## pendant :3968
##
##
## SporePrintColor Population Habitat
## white :2388 abundant : 384 wood :3148
## brown :1968 clustered: 340 grasses:2148
## black :1872 numerous : 400 leaves : 832
## chocolate:1632 scattered:1248 meadows: 292
## green : 72 several :4040 paths :1144
## buff : 48 solitary :1712 urban : 368
## (Other) : 144 waste : 192
Checking Frequency of mushroom classes
freq <- function(x){table(x)/length(x)*100}
freq(mushroom$Edibility)
## x
## edible poisonous
## 51.79714 48.20286
Poisonous & Edible classes are almost balanced.
Bar Charts comparing Edibility across all mushroom features
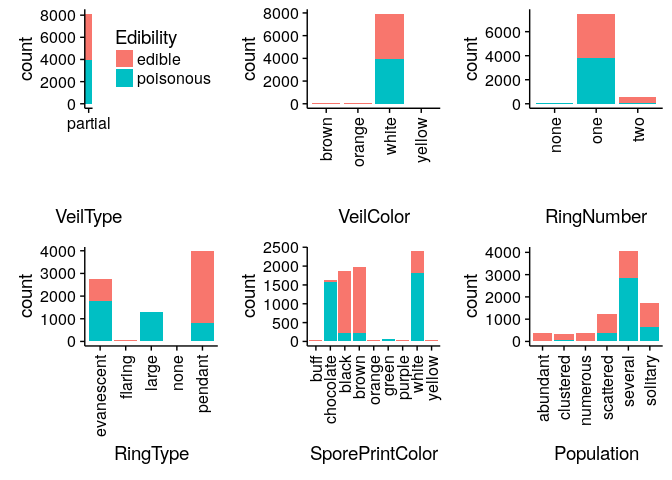
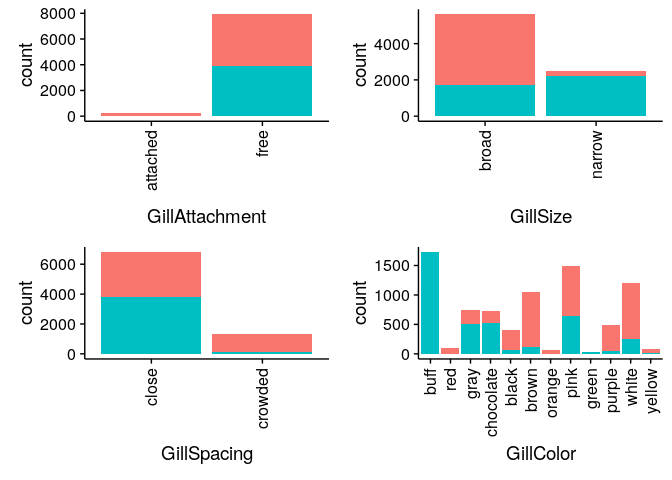
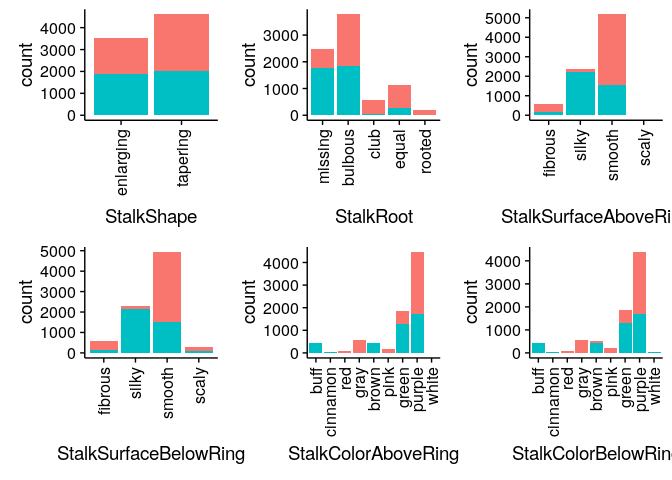
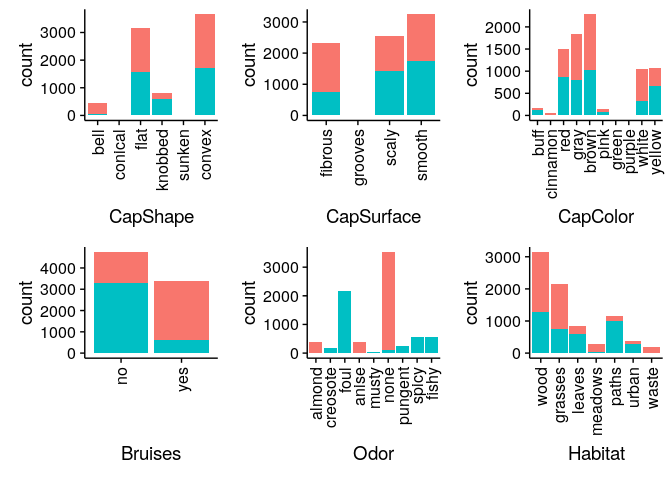
Classifying Mushrooms:
Creating Train Test Splits
I will take 70% (5386 mushrooms) sample data for training & 30% (2438 mushrooms) for testing.
set.seed(2)
s=sample(1:nrow(mushroom),0.7*nrow(mushroom))
mush_train=mushroom[s,]
mush_test=mushroom[-s,]
mush_test1<- mush_test[, -1]
Creating Model using Naive Bayes Classifier
Naive Bayes classifier is based on Bayes Theorem with an assumption of independence among predictors. In simple terms, a Naive Bayes classifier assumes that the presence of a particular feature in a class is unrelated to the presence of any other feature.
model <- naiveBayes(Edibility ~. , data = mush_train)
Predicting Mushroom Class on Testset
Lets test our model on remaining 30% test data
pred <- predict(model, mush_test1)
Model Evaluation
confusionMatrix(pred,mush_test$Edibility)
## Confusion Matrix and Statistics
##
## Reference
## Prediction edible poisonous
## edible 1245 147
## poisonous 9 1037
##
## Accuracy : 0.936
## 95% CI : (0.9256, 0.9454)
## No Information Rate : 0.5144
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.8715
## Mcnemar's Test P-Value : < 2.2e-16
##
## Sensitivity : 0.9928
## Specificity : 0.8758
## Pos Pred Value : 0.8944
## Neg Pred Value : 0.9914
## Prevalence : 0.5144
## Detection Rate : 0.5107
## Detection Prevalence : 0.5710
## Balanced Accuracy : 0.9343
##
## 'Positive' Class : edible
##
In case of mushroom classification few False Negatives are tolerable but even a single False Positive can take someones life. We measure these as Sensitivity & Specificity.
We are getting Sensitivity(True Positive Rate) of 99.28% which is good as it represent our prediction for edible mushrooms & only .7% False negatives(9 Mushrooms).
But Specificity(True Negative Rate) or our ability to classify Poisonous mushrooms is 87.58%, which is not so good as more then 10% Poisonous mushrooms may get identified as Edible. This model have 147 False Positives which is not acceptable. so lets try a decision tree based model now.
Creating a Decision Tree based Classifier
Decision tree is a type of supervised learning algorithm works for both categorical and continuous input and output variables. In this technique, we split the population or sample into two or more homogeneous sets (or sub-populations) based on most significant splitter / differentiator in input variables.
tree.model <- rpart(Edibility ~ .,data = mush_train,method = "class",parms = list(split ="information"))
#prp(tree.model)
#summary(tree.model)
rpart.plot(tree.model,extra = 3,fallen.leaves = T)

tree.predict <- predict(tree.model, mush_test[,-c(1)], type = "class")
confusionMatrix(mush_test$Edibility, tree.predict)
## Confusion Matrix and Statistics
##
## Reference
## Prediction edible poisonous
## edible 1254 0
## poisonous 16 1168
##
## Accuracy : 0.9934
## 95% CI : (0.9894, 0.9962)
## No Information Rate : 0.5209
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.9869
## Mcnemar's Test P-Value : 0.0001768
##
## Sensitivity : 0.9874
## Specificity : 1.0000
## Pos Pred Value : 1.0000
## Neg Pred Value : 0.9865
## Prevalence : 0.5209
## Detection Rate : 0.5144
## Detection Prevalence : 0.5144
## Balanced Accuracy : 0.9937
##
## 'Positive' Class : edible
##
This model gives us an ideal Specificity of 1 but Decision Trees are prone to overfitting & so model may perform poorly on test data. Also algorithm have chosen only 2 attributes Order & SporePrintColor for making this prediction which might be questionable. Lets also try a final model called Random Forest which is robust & often gives a more generalizable model.
Creating Random Forest Classifier
Random forests are an ensemble learning method for classification, regression and other tasks, that operate by constructing a multitude of decision trees at training time and outputting the class that is the mode of the classes (classification) or mean prediction (regression) of the individual trees.
set.seed(1234)
rf_model <- randomForest(Edibility~.,data=mush_train, importance = TRUE, ntree = 1000)
rf_model
##
## Call:
## randomForest(formula = Edibility ~ ., data = mush_train, importance = TRUE, ntree = 1000)
## Type of random forest: classification
## Number of trees: 1000
## No. of variables tried at each split: 4
##
## OOB estimate of error rate: 0%
## Confusion matrix:
## edible poisonous class.error
## edible 2954 0 0
## poisonous 0 2732 0
varImpPlot(rf_model)
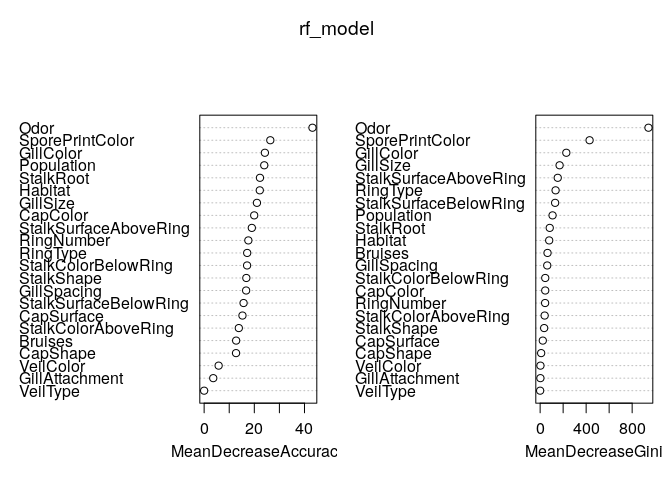
Random forest of 1000 trees have also identified Odor & SporePrintColor as most important variables. Lets check its predictions on test data now.
rf_prediction <- predict(rf_model, mush_test[,-c(1)])
confusionMatrix(mush_test$Edibility, rf_prediction)
## Confusion Matrix and Statistics
##
## Reference
## Prediction edible poisonous
## edible 1254 0
## poisonous 0 1184
##
## Accuracy : 1
## 95% CI : (0.9985, 1)
## No Information Rate : 0.5144
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 1
## Mcnemar's Test P-Value : NA
##
## Sensitivity : 1.0000
## Specificity : 1.0000
## Pos Pred Value : 1.0000
## Neg Pred Value : 1.0000
## Prevalence : 0.5144
## Detection Rate : 0.5144
## Detection Prevalence : 0.5144
## Balanced Accuracy : 1.0000
##
## 'Positive' Class : edible
##
We are getting 100% Accuracy, Sensitivity & Specificity now. I am not
sure if this is correct. Please share your feedback on errors &
improvements. Thanks for reading this notebook.